Walaupun persamaan yang diperkenalkan oleh Albert Einstein, E=mc² paling dikenali ramai tetapi mengikut kajian yang telah dibuat oleh Live Science, mereka tidak menyenaraikan persamaan tersebut sebagai satu persamaan yang cantik dan indah. Pihak Live Sceince telah membuat kaji selidik keatas ahli-ahli fizik, angkasawan dan ahli-ahli matematik dan berikut adalah sepuluh persamaan matematik yang paling indah bagi mereka.
1. Kerelatifan Am (General relativity)
Kerelatifan am merupakan teori geometri tentang kegravitian yang diterbitkan oleh Albert Einstein pada 1915. Ia menyatukan kerelatifan khas dan hukum kegravitian semesta Isaac Newton yang memperlihatkan graviti bukan dari sudut daya (seperti pendapat tradisi) tetapi lebih kepada manifestasi lengkungan masa dan ruang yang dihasilkan oleh jisim-tenaga bagi ruang-masa.
2. Model Piawai (Standard Model)
Model Piawai fizik zarah merupakan teori tiga daripada empat interaksi asas zarah yang diketahui. Zarah-zarah ini menyempurnakan segala jirim yang terdapat di alam semesta. Setiap eksperimen berkaitan dengan fizik kuasa tinggi yang dijalankan sejak pertengahan abad ke-20 jelas mempamerkan hasil yang sama dan konsisten iaitu, Model Piawai. Namun begitu, Model Piawai tetap bukanlah teori interaksi asas kerana model ini tidak termasuk graviti, jirim gelap dan tenaga gelap.
3. Kalkulus (Calculus)
Kalkulus (Bahasa Latin: calculus, ertinya "batu kecil" untuk menghitung) adalah cabang ilmu matematik yang merangkumi had, terbitan, kamiran, dan deret tak terhingga. Kalkulus adalah ilmu mengenai perubahan, sebagaimana geometri adalah ilmu mengenai bentuk dan algebra adalah ilmu mengenai pengerjaan untuk memecahkan persamaan serta aplikasinya. Kalkulus mempunyai aplikasi yang luas dalam bidang-bidang sains, ekonomi, dan teknikal; serta dapat menyelesaikan pelbagai masalah yang tidak dapat diselesaikan dengan algebra asas.
Kalkulus mempunyai dua cabang utama, iaitu kalkulus pembezaan dan kalkulus kamiran yang saling berhubungan melalui teorem asas kalkulus. Pelajaran kalkulus adalah pintu gerbang menuju pelajaran matematik lain yang lebih tinggi, yang khusus mempelajari fungsi dan limit, yang secara umum dinamakan analisis matematik
4. Teorem Phitagoras (Pythagoras theorem)
Dalam bidang matematik (geometri), teorem Pythagoras ialah teorem yang mengaitkan ketiga-tiga sisi dalam segi tiga bersudut tepat. Menurut teorem ini, kuasa dua bagi bagi hipotenus (garisan sendeng) segi tiga bersusut tepat adalah sama dengan hasil tambah kuasa dua bagi dua sisi lain.
Katakan bahawa c ialah panjang hipotenus, manakala a dan b pula ialah panjang dua sisi yang berbaki, persamaan berikut boleh dibuat:
dan c dapat dirumuskan sebagai:
 |
| sumber Math is Fun |
5. 1 = 0.999999999….
Ini adalah persamaan yang mudah yang mana menyatakan 0.9999 yang diikuti dengan angka sembilan syang tiada penghujung adalah sama dengan satu, 1, menjadi kegemaran kepada ahli matematik bernama
Steven Strogatz dari Universiti Cornell.- "I love how simple it is — everyone understands what it says — yet how provocative it is," kata Strogatz . "Many people don't believe it could be true. It's also beautifully balanced. The left side represents the beginning of mathematics; the right side represents the mysteries of infinity."
- Dalam matematik, perpuluhan berulang 0.999…, yang juga ditulis sebagai
 atau
atau  , menandakan sebuah nombor nyata sama dengan nombor 1. Dalam maksud lain, "0.999…" mewakili nombor yang sama dengan simbol "1". Persamaan ini telah lama diterima oleh ahli matematik profesional dan diajar di dalam buku-buku teks. Berbagai-bagai bukti matematik terhadap identiti ini telah dirumuskan dengan bermacam-macam kekerasan matematik, tumbesaran nombor nyata yang diutamakan, andaian latar belakang, kandungan sejarah dan kumpulan sasaran masyarakat.
, menandakan sebuah nombor nyata sama dengan nombor 1. Dalam maksud lain, "0.999…" mewakili nombor yang sama dengan simbol "1". Persamaan ini telah lama diterima oleh ahli matematik profesional dan diajar di dalam buku-buku teks. Berbagai-bagai bukti matematik terhadap identiti ini telah dirumuskan dengan bermacam-macam kekerasan matematik, tumbesaran nombor nyata yang diutamakan, andaian latar belakang, kandungan sejarah dan kumpulan sasaran masyarakat.
6. Kerelatifan khas (Special relativity)
Kerelatifan khas atau teori kerelatifan khas merupakan teori fizik yang diterbitkan pada 1905 oleh Albert Einstein dalam rencananya "Mengenai Elektrodinamik Jasad yang Bergerak" (bahasa Inggeris: "On the Electrodynamics of Moving Bodies"). Teori tersebut menggantikan tanggapan Newton tentang ruang dan masa dan melibatkan electromagnet seperti yang diwakilkan dalampersamaan Maxwell. Teori ini dipanggil "khas" kerana ia melibatkan prinsip kerelatifan hanya pada keadaan tertentu bagi kerangka rujukan inersia dalam ruang masa yang mendatar dan kerangka yang terpecut, iaitu ketika kesan graviti boleh diabaikan.
Kerelatifan khas menghubungkaitkan ruang dan masa ketika laju cahaya (begitu juga pemalar asas yang lain) adalah malar, dan teori membawa kepada satu keadaan ketika dua pemerhati boleh bercanggah tentang selang masa dan jarak di antara dua kejadian, tetapi tanpa bercanggah kejadian yang berlaku. Hal tersebut menunjukkan yang masa boleh berlalu lebih perlahan jika pemerhati bergerak, bergantung kepada laju relatif.
Teori ini turut meramalkan persamaan E=mc².
 |
| sumber: Live Science |
7. Persamaan Eular (Eular's Equation)
Identiti Euler atau persamaan Euler, yang mendapat namanya daripada ahli matematik berbangsa Switzerland-Jerman Leonhard Euler, ialah persamaan
di mana
 ialah nombor Euler, iaitu asas bagi logaritma asli,
ialah nombor Euler, iaitu asas bagi logaritma asli,
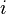 ialah unit khayalan, iaitu punca kuasa dua −1, dan
ialah unit khayalan, iaitu punca kuasa dua −1, dan
 ialah pi, iaitu nisbah antara ukur lilit sebuah bulatan dan diameternya.
ialah pi, iaitu nisbah antara ukur lilit sebuah bulatan dan diameternya.
Identiti Euler dianggap sebagai salah satu persamaan paling indah dalam matematik. Persamaan ini mengandungi tiga operasi matematik yang setiap satunya digunakan satu kali sahaja:tambah, darab, dan eksponen. Persamaan ini juga merangkai lima pemalar matematik paling asas:
- 0, iaitu "identiti penambahan".
- 1, iaitu "identiti pendaraban".
- π (3.14159265...), yang lazim digunakan dalam ilmu trigonometri, geometri ruang Euclid, dan analisis matematik.
- e (2.718281828...), asas bagi logaritma asli, yang lazim digunakan dalam analisis matematik dan sains. Kedua-dua π dan e adalah nombor transenden.
- i, iaitu unit khayalan bagi nombor kompleks, iaitu set nombor yang mengandungi punca kuasa dua bagi semua polinomial (yang bukan pemalar), dan kajian mengenainya mendorong kepada penerokaan yang lebih mendalam pada bidang-bidang berkenaan algebra dan kalkulus.
8. Teorem Noether dan Persamaan Eular- Lagrange (Euler–Lagrange equations and Noether's theorem)
"Ini adalah agak abstrak tetapi sangat menakjubkan," kata Cranmer NYU. "Perkara yang hebat adalah cara berfikir tentang fizik telah membawa kepada beberapa revolusi utama dalam fizik, seperti mekanik kuantum, relativiti, dan lain-lain"
Di sini, L bermaksud untuk Lagrangian, yang merupakan ukuran tenaga dalam sistem fizikal, seperti mata air, atau tuil atau zarah asas. "Penyelesaian persamaan ini memberitahu anda bagaimana sistem akan berubah dengan masa," kata Cranmer.
Satu spinoff persamaan Lagrangian dipanggil teorem Noether, selepas abad ke-20 Jerman Emmy Noether matematik. "Teorem ini adalah benar-benar asas kepada fizik dan peranan simetri," kata Cranmer. "Secara tidak rasmi, teorem ini mengatakan jika sistem anda mempunyai simetri, maka terdapat perkaitan dengan hukum keabadian. Sebagai contoh, idea bahawa hukum asas fizik hari ini adalah sama dengan esok (masa simetri) membayangkan bahawa tenaga diabadikan.Idea bahawa hukum fizik adalah sama di sini kerana mereka berada di angkasa lepas menunjukkan momentum yang diabadikan. Simetri adalah mungkin konsep memandu dalam fizik asas, terutamanya disebabkan oleh sumbangan Noether. "
9. Persamaan Callan-Symanzik (The Callan-Symanzik equation)
Dalam fizik, persamaan Callan-Symanzik merupakan persamaan kebezaan yang menggambarkan evolusi fungsi korelasi n-titik di bawah perubahan skala tenaga di mana teori ditakrifkan dan melibatkan beta fungsi teori dan dimensi ganjil. Persamaan ini mempunyai struktur berikut
dimana
 adalah fungsi beta
adalah fungsi beta  adalah scaling of the fields.
adalah scaling of the fields.
Dalam kuantum elektrodinamik persamaan ini mengambil bentuk
10. Persamaan Permukaan Minima (The minimal surface equation)
Dalam matematik, permukaan minimum adalah permukaan yang meminumkan kawasan persekitarannya. Ini adalah bersamaan dengan kelengkungan min sifar.
Istilah "permukaan minimum" digunakan kerana permukaan ini asalnya wujud sebagai permukaan yang mengurangkan jumlah luas permukaan tertakluk kepada kekangan tertentu.
Model fizikal kawasan-meminimumkan permukaan minimum boleh dibuat dengan mencelup bingkai dawai ke dalam larutan sabun, membentuk sebuah filem sabun, yang adalah permukaan minimum yang sempadan adalah bingkai dawai.
Walau bagaimanapun istilah ini digunakan untuk permukaan yang lebih umum yang mungkin sendiri bersilang atau tidak mempunyai kekangan. Untuk kekangan diberikan terdapat juga mungkin wujud permukaan yang minimum dengan beberapa kawasan yang berbeza (contohnya, melihat permukaan minimum revolusi): definisi standard hanya berkaitan dengan optimum tempatan, tidak optimum global.
sumber
1. Yahoo!
2. Wikipedia
3. lain-lain yang telah dinyatakan : D
* maaf banyak guna google translate..heheheee...
almaklumlah ta pandai sangat nak terjemah sendiri..






![\left[M\frac{\partial }{\partial M}+\beta(g)\frac{\partial }{\partial g}+n\gamma\right] G^{(n)}(x_1,x_2,\ldots,x_n;M,g)=0](http://upload.wikimedia.org/math/1/2/2/122fb77715bddbe3cea0015d8f987a90.png)
![\left[M\frac{\partial }{\partial M}+\beta(e)\frac{\partial }{\partial e}+n\gamma_2 +m\gamma_3\right]G^{(n,m)}(x_1,x_2,\ldots,x_n;M,e)=0](http://upload.wikimedia.org/math/4/e/b/4eb6a40f663017902a5dfcf7d1c92b19.png)

No comments:
Post a Comment